Hierarchical Graph Pooling with Structure Learning

arXiv

---

Hierarchical Graph Pooling with Structure Learning

---

Zhen Zhang1 , Jiajun Bu1 , Martin Ester2 , Jianfeng Zhang3 , Chengwei Yao1 , Zhi Yu1 , Can Wang1

---

본 논문은 graph neural networks(GNN)에서 pooling을 적용하기 위한 논문으로 node간의 중요한 연결은 유지하면서 약한 연결은 제거하고, 계산량이 너무 많아지지 않는 방법을 제안한 논문이다.

Graph structure는 기존에 사양되던 분야를 넘어 Vision Graph Neural Network (ViG) 등의 등장으로 vision 분야에도 활용을 하기위한 연구가 활발하다. grpah를 통해 image의 obejct를 flexible하게 찾을 수 있기 때문에 좋은 영향을 끼칠수 있는 기술이라 생각한다.

Doi : https://doi.org/10.48550/arXiv.1911.05954

Hierarchical Graph Pooling with Structure Learning

---

1. Introduction

---

Convolution과 pooling layer를 활용한 deep neural network는 computer vision, nature language understanding, video processing 등 다양한 tasks에서 뛰어난 성능 향상을 보이고 있다. 이러한 task는 일반적으로 Euclidian space의 형태로 표현할 수 있어 대부분 convolution 연산의 지역성(locality) 및 순서 정보(order information)를 포함하고 있다.

 

이와 같은 표현 방법은 real-world에서 많은 문제를 가지게 된다고 한다. 예를 들어 social networks, chemical molecules, biological network 등과 같은 많은 양의 데이터가 graph structure로 자연스럽게 표현되는 non-Euclidian domain이기 때문이다. 그러나 이러한 문제로 convolution, pooling 연산을 사용하지 않기에는 일반화 성능이 너무 뛰어나다. 그렇기 때문에 graph structure에 convolution 연산을 적용하기 위한 연구가 많이 진행되었다.

 

1.1 Graph Convolution

현재는 graph neural network를 통해 convolution 연산은 graph problem에 generalized 되었다.

일반적으로 graph classification을 진행하기 위한 방법은 크게 spectral과 spatial 접근법 두 가지 방법으로 나눌 수 있다.

Method	방법 설명
Spectral Method	Graph Furier transform을 based로 graph convolution을 정의
Spatial Method	graph convoltuion을 이웃에서 직접 node 표현을 aggregating하여 연산

위에서 설명한 두 가지 방법은 대부분 주로 메시지 전달 체계에 적합할 수 있는 있는 graph 전반에 걸쳐 node feautre를 transforming, propagtain, aggregating 하는 것을 포함한다.

GNN은 다양한 유형의 graph에 적용되어 node classification, link prediction, recommendation 등을 포함한 수많은 graph 관련 작업에서 뛰어난 성능을 얻었다.

 

1.2 Graph Pooling

계층적 표현을 학습하는 것이 graph classification에서 중요하지만 graph pooling은 아직 많이 연구되지 않았다.

 

그럼 Graph classification의 목표는 뭘까?

Graph classification의 목표는 node features와 graph structure information을 활용하여 graph와 관련된 label을 예측하는 것으로 이는 graph classfication을 위해서는 graph level 표현이 필요하다는 것을 의미한다.

 

기존의 GNN은 node level 표현을 많이 사용하였다. 그래서 node 표현을 globally summarize하는 방법으로 graph level에 접근하는 방식을 많이 사용하였다고 한다. 이 과정에서 graph 전체 구조 정보가 무시되기 때문에, 이 방법을 통해 생성된 graph level 표현은 "flat"해진다. 또한 GNN은 edge를 통해 node간의 메시지를 전달할 수 있을 뿐 계측적 방식으로 node를 쉽게 aggregate할 수 없다.

 

graph는 종종 다른 substructures를 가지며 node는 다른 역할을 하므로 graph level 표현에 다른게 기여를 해야한다.

예를 들어 protein-protein interaction graphs의 경우 특정 하위 구조는 전체 graph의 특성을 예측하는데 매우 중요한 특정 feature를 나타낼 수 있따. 그러므로 graph의 loacl 및 global structure information을 모두 캡처하려면 hierarchical pooling(계층적 풀링) process가 필요하다.

 

1.3 Hierarchical Graph Pooling

GNN의 hierarchical pooling에 초점을 맞춘 연구들이 최근에 많이 진행되고 있다. 이러한 model들은 일반적으로 grouping 혹인 sampling node를 통해서 graph를 subgraph로 만들기 때문에 전체 graph 정보는 단계적으로 hierarchical induced subgraph(계층적 유도 하위 그래프) 정보로 줄어들게 된다.

이렇게 subgraph를 생성하는 방식에는 두 가지 문제점이 존재한다.

• 높은 computational complexity
• 생성된 induced subgraph는 주요 subgraph를 보존하지 못하고 결국 graph topological information의 완전성을 잃을 수 있다.

예를 들어, 직접 연결되지 않았지만 원래 graph에서 많은 공통 이웃을 공유하는 두 node는 직관적으로 subgraph에서 가까워야하는데 유도된 subgraph에서는 서로 도달할 수 없게 될 수 있다. 이러한 왜곡된 graph structure는 후속 layer에서 메시지 전달을 방해하게 된고 한다.

 

이러한 문제점을 해결하기 위해서 이들은 새로운 graph pooling operator인 HGP-SL을 제안하고 있다.

HGP-SL은 hierarchical graph level representations를 학습하게 된다.

이들이 제안하는 방법의 contribution을 정리하면 다음과 같다.

• HGP-SL은 먼저 정의된 node information score에 따라 adaptive하게 subset을 선택하는데, 이 score는 node feature와 graph topological information을 모두 완전히 활용한다
• 들이 제안한 방법은 non-parametric step이므로 이 절차 중에 추가 parameters를 최적화할 필요가 없다. 그렇기 때문에 이는 CNN의 pooling과 비슷하며, 구현하기가 쉽다는 장점이 있다.
• graph의 주요 sub-structures를 보존하기 위해 poolied graph에 sparse attention을 적용하였다.
• pooling operator를 graph convolutional neural network에 통합하여 graph classification을 수행하며 전체 절차를 end-to-end 방식으로 최적화할 수 있다.

---

2. The Proposed Model

---

2.1 Notations and Problem Formulation

graph data G = {G_1, G_2, ..., G_n} 이때, 각 graph의 node 및 edge 수가 많이 다를 수 있다.

임의의 graph G_i = ( V_i , E_i , X_i ), n_i와 e_i는 각각 node와 edge의 수를 나타낸다.

A_i ∈ R^(n_i × n_i) 는 연결 정보를 설명하는 인접행렬이며 X_i ∈ R^(n_i × f)는 node feature 행렬을 나타내면, 여기서 f는 node 속성의 차원이다.

 

Label matrix Y ∈ R^(n × c) 는 각 graph에 대한 관련 label을 나타낸다. 즉, G_i가 class j에 속하면 Y_i = 1이고, 그렇지 않으면 Y_i = 0 이다.

 

Graph pooling 작업으로 인해 graph structure와 node numbers가 layers 간에 변경되므로 k-th layer에 공급되는 i번째 graph를

위와 같은 node를 사용하여 G{ _i}{ ^k} 로 추가로 나타낸다.

그런 다음 인접 행렬과 hidden representation matrix는

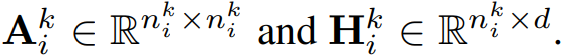
위와 같이 표현할 수 있다.

이 표기법을 활용하여 문제를 정의하면 다음과 같이 정의할 수 있다.

Input	Label 정보 Y_L이 있는 graph G_L 집합이 주어지면 graph neural network layers K의 수, pooling ratio r, 각 layer의 representation dimension d
Output	end-to-end 방식으로 graph neural network를 사용하여 G/G_L 의 알려지지 않은 graph label을 예측하는 것

 

2.2 The Overall Neural Network Architecture

Figure 1 은 이들이 제안하는 『Hierarchical Graph Pooling wiht Structure Learning (HGP-SL)』 의 overview이다.

HGP-SL은 graph convolution operations 사이에 graph pooling operations가 추가되는 graph nueral network work의 형태이다.

이들이 제안하는 방법에서의 주요 component는 크게 두 가지로 볼 수 있다.

• subset의 informative node를 보존하고 더 작은 induced subgraph를 유도하는 graph pooling
• pooling된 subgraph에 대한 정제된 graph structure를 학습하는 structure learning

pooling이 진행되면 정보가 희석될 수가 있는데, 이들이 제안하는 structure learning의 장점은 essentail graph structure information을 보존할 수 있다는 것이다.

이 정보가 보존되지 않으면 이웃 node에서 정보를 aggregating 할때 후속 alyer에서 정보 전파를 방해할 수가 있다고 한다.

 

전체 architecture는 convolution 및 pooling 작업의 stacking으로 graph representation을 hierarchical way로 학습할 수 있도록 하고 있다.

그런 다음 readout function을 이용하여 각 level의 node 표현을 요약하고, 최종 graph level 표현은 서로 다른 level의 요약을 추가하고 있다.

 

마지막으로 graph-level 표현은 softmax layer가 있는 MLP(Multi Layer Perceptron)으로 공급되어 graph classification을 수행한다.

 

그럼 이제 graph pooling과 structure learning에 대해서 세부적으로 알아보자!

 

2.3 Graph Pooling Operation

이들이 제안하는 graph pooling은 graph data에서 down sampling을 가능하게 한다.

이전의 graph pooling 작업은 새로보다 더 작은 graph를 형성하기 위해서 information node의 하위 집합을 식별하는데 이에서 영감을 받아 저자들은 node feature와 graph structure information을 모두 완전히 활용할 수 있는 non-parametric pooling operation을 설계하였다.

 

이들이 제안하는 방법의 핵심은 node 선택 절차에서 node를 선택하는 기준을 정하였다는 것이다. node sampling을 수행하기 위해서는 먼저 node에 포함된 정보를 평가하게 되는데 이때 평가하는데 node information score라는 기준을 도입하였다.

 

일반적으로 node의 표현이 이웃표현으로 재구성될 수 있다면, 정보의 손실이 거의 없는 pooling된 graph에서 이 node는 삭제가 가능하다. 이때 node representation과 하나의 이웃간의 거리를 Mahattan distance(L1 distance)로 구하여 node information score로 사용하게 된다.

 

node representation과 이웃 node로 구성된 Mahattan distance를 수식으로 표현하면 다음과 같다.

다음 수식에서

는 각각 인접행렬과 node resentations 행렬을 나타낸 것이다.

|| ||_1 이 수식은 L1 norm 이다.

D^{k}_{i} 는 A^{k}_{i} 의 대각행렬을 의미한다.

I^{k}_{i}는 identity matrix를 의미하며 p ∈ R^(n_i) 는 information socre이다.

 

Node information score를 흭득한 후, 이제 pooling operation에 의해 보존되어야하는 node를 선택하능하게 되는데 graph information을 근사화하기 위해서는 이웃으로 잘 표현할 수 없는 node들만 보존을 하게 된다. 즉, node information score가 상대적으로 큰 node는 더 많은 정보를 제공할 수 있다고 판단하여 pooling된 graph의 구성에서 보존이 되는 것이다.

 

node information score에 따라 graph의 node 순서를 변경한 다음 top_ranked nodes의 subset를 선택하게 된다.

 

이들이 제안하는 graph pooling을 요약하면 다음과 같이 정리할 수 있다.

---

• node 선택 절차에서 node를 선택하기 위한 기준을 정의한다.
• node sampling을 수행하기 위해서 먼저 node에 포함된 정보를 평가하는데 이때 node information score라는 기준을 도입하였다.
• 일반적으로 node의 표현이 이웃표현으로 재구성될 수 있다면, 그 node는 정보의 손실이 거의 없는 pooling된 graph에서 제거가 가능하다.
• node 표현과 하나의 이웃간의 거리를 Manhattan distance(L1 distance)로 구하여 node information score로 사용한다.
• graph information을 근사화하기 위해서는 이웃으로 잘 표현할 수 없는 node들만 보존한다. 즉, node information score가 상대적으로 큰 node는 더 많은 정보를 제공할 수 있다고 판단하여 pooling된 graph의 구성에서 보존이 된다.

---

2.4 Structure Learning Mechanism

이들이 제안하는 structure learning은 pooling된 graph에서 정제된 graph structure를 학습하는 것이다.

Pooling operation이 수행되면 subgraph에서 관련성이 높은 node가 연결이 해제되어 graph structure 정보의 완전성이 손실되고 메시지 전달 절차가 어려워질 수가 있다. 이러한 문제점을 개선하기 위해서 structure learning이 필요하다고 저자들은 이야기하고 있다.

 

graph structure를 얻는 기존의 방법은 두 가지가 있었다.

• Domain knowledge (e.g. social network)
• 사람이 설정한 graph (e.g. KNN graph)

하지만 이 두방법은 일반적으로 손실되거나 noise가 많은 정보들 때문에 graph neural network의 학습 작업에 적합하지 않다.

 

이러한 문제를 개선하기 위해서 approximate distance metric learning algorithm이 등장하였다. 이 algorithm을 사용하여 graph Laplacian을 adaptive하게 주정하는 방법이 제안되었다.

approximate distance metric learning algorithm이 node label estimation을 위해서 구성된 graph 구조를 학습하기 위해서 도입이 되었지만 해당 algorithm같은 경우 밀도가 높은 연결된 graph를 생성하기 때문에 hierarchical graph level representation learning scenario에 적합하지 않다는 문제점이 발생하였다.

 

그래서 본 논문의 저자들은 sparse attention을 활용한 sparse graph structure를 학습하는 생로운 structure learning layer를 제안하고 있다.

 

제안하는 방법에 대해서 그럼 알아보도록 하자.

Graph G_i를 pooling하게 되면 G^(k)_(i) 를 얻게 되는데 이것은 k-th layer에 있는 pooling된 graph를 의미한다.

수식

는 각각 structure information과 hidden information을 의미하는데 이 두 개를 input으로 사용하게 된다.

최종적인 이들의 목적은 "각 node 쌍 사이의 기본 쌍 관계를 encoding하는 정제된 graph structure를 학습시는 것" 이다.

 

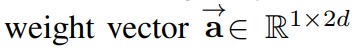
이들은 위와 같은 weight vector에 의해 parameterized된 single layer neural network를 활용하였다고 한다.

그런 다음 attention mechanism에 의해 계산된 node v_p와 v_q 사이의 similiarity score는 아래의 수식과 같이 표현할 수 있다.

σ(·) : activation function like ReLU(·)

|| : concatenation operation

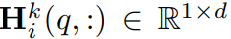
는 각각 node v_p와 v_q의 표현을 나타내는 행렬 H^(k)_(i) 의 p-th와 q-th 행을 나타낸다.

는 유도된 subgraph를 encoding 한 것인데 이때 이 값이 0 이면 node v_p와 v_q가 직접 연결이라는 의미이다.

이 식을 structure learning layer에 통합하여 직접 연결된 node간에 비교적 큰 similarity scoe를 주기위해 bias 시키고, 동시에 직접 연결되지 않은 node간의 기본 쌍 관계를 학습하려고 한다.

λ 는 이 node간의 trade-off parameter 이다.

 

similarity score는 softmax를 통해 정규화 되게 된다.

하지만 softmax의 값은 항상 0이 아닌 숫자를 가지고, 따라서 fully connected graph를 만들어 학습에 많은 noise가 생길수도 있다는 문제점이 있다.

 

이를 보완하기 위해서 저자들은 softmax function이 가지고 있는 대부분의 특성은 유지하고 희소분포를 생성하는 sparsemax function을 사용하는 것을 제안하고 있다.

이는 아래와 같은 수식으로 나타낼 수 있다.

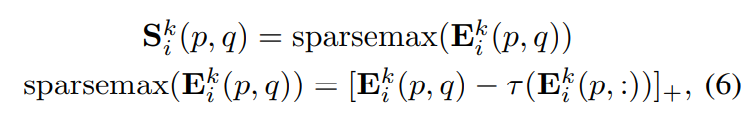
[x]_+ = max{0, x}

τ (·) = threshold function that returns a threshold according to the procedure shown in Algorithm 1.

따라서 sparsemax(·) 는 threshold 이상의 값을 유지하고 다른 값은 0으로 잘려 희소 그래프 구조(sparse graph structure)를 가져오게 된다.

 

2.5 Improving Structure Learning Efficiency

Large scale graphs의 경우 structure S^(k)_(i) 를 학습하는 동안 각 node쌍 간의 similarity를 계산하는데 너무 많은 계산 비용이 들것이다. 그렇기 때문에 graph의 localization과 smoothness 특성을 추가로 고려하여 node의 h-hop neighborhood(h=2 or 3) 내에서 계산 process를 제한하는 것이 합리적이라고 본 저자들을 말하고 있다. 이렇게 제한을 하게 되면 계산비용이 크게 줄어들 것이다.

---

3. Experiments and Analysis

---

다양한 dataset에 대해서 기존의 방법들과 비교실험을 진행한 결과 이들이 제안하고 있는 모델의 성능이 가장 좋음을 확인할 수 있다.

Table 3을 통해 이들이 제안하는 SL을 다양한 backbone에 적용을 하였을 때의 성능을 확인할 수 있다. 이때 HGP-SL이 가장 좋은 성능을 보이고 있다.

 

Figure 2는 Hyper-parameter에 따른 성능 비교이다.

 

이들은 networkx 를 사용하여  HGP-SL과 이것의 다른 변형들의 pooling 결과를 시각화 하였다.

154개의 node를 포함하는 protein dataset에서 무작위로 graph를 sampling한 것이라 한다.

pooling ratio가 0.5로 설정된 three pooled graph neural network를 구성한 다음 node가 각각 77, 39, 20인 3개의 pooling graph를 생성하였다.

 

figure 3를 통해서 HGP-SL(DEN)은 의미 있는 graph topologies를 보존하지 못한 반면 HGP-SL은 pooling후 원래 protein graph의 비교적 합리적인 topology를 보존할 수 있음을 확인할 수 있다.

---

4. 정리

---

해당 논문의 중요한 점을 간단히 정리해보자면 다음과 같다.

 

1. graph pooling

• Manhattan distance로 거리를 구해 node information score로 사용하고 이 값이 높을수록 더 많은 정보를 준다고 판단하여 보존이 된다.
• 이웃 node로 표현되는 node는 제거해도 된다.

2. Structure learning

• Similarity score로 sturecture를 구성하고 학습한다.
• softmax 대신에 sparsemax를 사용한다.
• sparse attention 개념이 적용되었다.

 

본 논문에서 제안한 방법은 효과적으로 graph를 sampling하고 중요한 정보를 추출하는 방법이라고 생각한다.

이러한 방법은 다양한 graph 구조에서 좋은 성능 향상을 가져올 수 있을 것이라고 생각하기 때문에 실험을 진행해볼 예정이다.