Self-attention does not need O(n^2) memory

Arxiv

---

Self-attention does not need O(n^2) memory

---

Google Research

---

Attention is all you need를 통해서 소개된 self-attention은 transformer model의 core이며 엄청난 성능을 보여주고 있다.
이를 활용하여 NLP 분야에서는 GPT가 등장하였으며 vision 분야에서는 vision transformer(ViT)의 등장으로 기존의 cnn을 능가하는 성능을 보이고 있다. 그러나 self-attention은 O(n^2) 만큼의 시간복잡도와 공간복잡도를 요구한다는 큰 문제점을 가지고 있다. 그중 본 논문은 공간복잡도를 개선하는 방법을 소개하는 논문이다. 기존 수식의 변화 없이, 즉 기존 self-attnetion 메커니즘에는 변화를 주지 않고 단순히 계산의 순서만 바꾸는 트릭을 이용하여 기존의 성능에 변화 없이 메모리 복잡도를 줄인 논문이다.
Doi : arXiv:2112.05682

Self-attention Does Not Need $O(n^2)$ Memory

 

---

1. Introduction

Attention은 neural architecutre에서 폭넓게 사용되고 있다. 그중에서 특히 transofmer의 core로 사용되는 self-attention은 NLP 분야에서 혁신을 일으키고 다른 분야에서 많이 채택되고 있는 방법이다.
 
Single query의 경우 attention의 결과로 value vector의 weighted sum을 얻는다. 이때 weight는 query와 key의 내적의 softmax값이다. 이를 수식으로 표현하면 아래와 같다.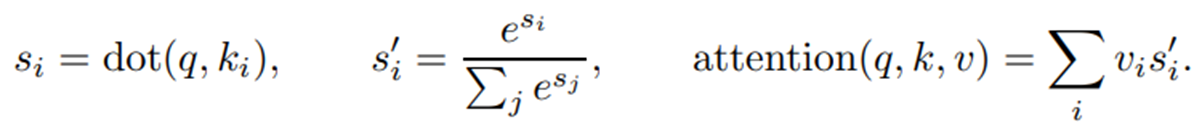

self-attention

 
그렇다면 single query인 경우 space complexity(공간 복잡도)는 어떻게 될까?
우선 single query에 대한 attention을 진행하기 위해서 모든 i에 대한 S_i (내적값)을 기억하고 있어야 한다. 그럼 결과적으로 space complexity가 O(n)이 될 것이다.
 
self-attention인 경우도 생각해보자.Transformer는 sequence 각 위치마다 별도의 query가 발생하는 self-attention을 사용하므로 기존 single query에서 O(n) 만큼의 memory가 query의 총 개수 n 만큼 더 필요하게 된다. 그러므로 space complexity가 O(n^2)이 된다.

---

Space complextiy of single query : O(n)
Space complexity of self-attention : O(n^2)

---

왜 space complexity가 중요한가?
본 저자들은 space complexity가 중요한 이유로 최근 accelerator hardware (GPUs, TPUs, etc.)는 대부분 deep learning에서 memory 사용은 제한적이지만 computation cost는 비교적 저렴하다고 이야기하고 있다.
이를 쉽게 이해하기 위해 Tesla A100과 GeForce RTX 4090을 비교해 보자

https://technical.city/en/video/Tesla-A100-vs-GeForce-RTX-4090

위 그림은 Tesla A100과 GeFore RTX 4090의 가격을 비교하는 그림이다. A100이 RTX 4090보다 대략 6~7배 정도 비싼 것을 확인할 수 있다.

https://timdettmers.com/2023/01/30/which-gpu-for-deep-learning/

이것은 stable defusion 성능을 gpu 마다 비교한 그래프이다.
위 두 그림을 통해 우리는 A100은 RTX 4090보다 용량을 크지만 computation은 더 좋지 않다는 것을 확인할 수 있다.
이를 통해 우리는 computation cost는 비교적 저렴하지만 memory를 늘리는 비용은 매우 비싸다는 것을 쉽게 확인할 수 있다.
 
이러한 memory 사용량의 문제를 algorithm 적으로 해결하고자 본 저자들이 제안하는 방법의 contribution은 아래와 같다.

---

Proposed

• Single query attention과 self-attention에서 각각 상수시간과 logarithmic memory만 필요로 한다.
• 기본 algorithm은 매우 간단하지만 수치적으로 실현가능하게 만드는 trick이 필요하다.
• TPU에서 효율적으로 실행되며 self-attention을 위해 O(√n) memory가 필요한 JAX로 구현한 방법을 소개한다.
• 기존 attention memory complexity를 줄이는 것을 목표로 하는 연구들과 달리, 이들이 제안하는 attentino에 대한 memory-efficient algorithm은 근사치가 아닌 동일한 함수를 계산한다.
• 이들이 제안하는 방법을 통해 architecture의 선택을 재고하거나 더 길거나 조밀한 attention이 필요한 새로운 dataset에 맞게 확장할 수 있다.
• Space complexity만 고려하였기 때문에 time complexity는 self-attention = O(n^2), single query attention = O(n)으로 변화가 없다.

---

비록 time complexity은 여전히 O(n^2)지만 space complexity를 줄이게 되면 더 긴 데이터를 처리할 수 있게 된다는 이점을 가지고 있으며 현재 accelerators에서는 연산 능력보다는 deivce의 memory가 제한적이게 문제가 되는 경우가 많다. 이는 long sequence data를 다루는 transformer에서 특히 큰 문제가 된다.

---

2. Algorithm

알고리즘을 확인하기 전에 간단하게 space complexity에 대해서 알아보고 가자.

---

Space complexity 란 프로그램을 실행시킨 후 완료하는데 필요로 하는 자원 공간의 양을 의미한다.
총 공간 요구 = (고정 공간 요구) + (가변 공간 요구)이다.
이때 고정 공간은 입력과 출력의 횟수나 크기와 관계없는 공간의 요구(코드 저장 공간, 단순 변수, 고정 크기의 구조 변수, 상수), 가변 공간은 해결하려는 문제의 특정 인스턴스에 의존하는 크기를 가진 구조화 변수들을 위해서 필요로 하는 공간, 함수가 순환 호출을 할 경우 요구되는 추가 공간, 그러니까 동적으로 필요한 공간을 의미한다.
 
수식으로 표현해 보면 S(P) = c + S_p(n)이며 이때, 고정 공간은 상수이므로 space complexity는 가변 공간에 좌우된다.

https://madplay.github.io/post/time-complexity-space-complexity

---

본 저자들은 sigle query attnetion을 위한 algorithm을 먼저 제시 후 self-attention으로 확장을 하는 방식으로 설명하고 있다.
Single query attention algorithm을 살펴보자.

기존 sigle query attention 수식

이때 수식 S'_i의 분모가 분배법칙을 통해 아래와 같이 분할될 수 있다.

수식 유도 과정

이러한 분배법칙을 통해 우리는 softmax 연산을 attention operation의 맨 끝으로 이동시킬 수 있다.
결과적으로 아래와 같은 수식을 얻게 되는 것이다.

위 수식은 사실 "lazy softmax"의 재발견이라고 한다. 이를 초기 제안한 연구자들은 space complexity를 focus 하여 연구를 진행하지 않았다. 그래서 이것을 발견하지 못했다고 한다.
본 논문 저자들은 이 수식을 통해 attention operation을 O(1), 즉 상수 memory로 계산이 가능토록 만들었다.
이때 해당 수식의 memory overhead는 vector v* ∈ R^d, vector s* ∈ R로 구성되며, 0으로 initialize 된다.
 
처리 순서를 정리해 보면 아래와 같다.

---

처리 순서

---

Space complexity 문제는 input이 특정 순서로 제공된다고 가정한다.
 
만약 특정 순서로 제공되지 않고 다른 순서로 제공된다면 어떻게 될까?
Index를 sequence에 추가로 저장해야 한다. 그렇기 때문에 O(log n)의 space complexity가 필요로 해진다.

---

O(log n) 유도

(유도 과정이 틀렸을 수도 있습니다 ㅠㅠ)

• sequence에 index의 한 칸의 공간이 더 필요해지게 된다.
• n -> n/2 -> n/4 ->... -> (n/2)^k : 계속 나눠지다 보면 결국 1이 될 것이다.
• (n/2)^k = 1 -> n = 2^k : 각 변에 log를 취하게 되면
• log n = k
• O(log n)의 space complexity가 된다.

---

self-attention의 경우 query에 대한 순차적인 연산들을 진행한 query 목록에 추가 index가 필요로 해진다.
이는 순서가 섞였을 경우와 동일한 문제로 O(log n)의 space complexity가 필요로 해진다.
 
최종 output으로 queries 수의 크기, 즉 O(n)의 linear output을 생성하지만 이것은 space complexity에 포함하지 않는다.

---

3. Numerical Stability

기존 attention과 이들이 제안하는 algorithm은 부동 소수점 산술을 사용할 때 수치적으로 안정적이지 않다는 문제가 있다. 이러한 문제는 softmax가 score를 지수화하기 때문에 발생한다.
예를 들어 score >= 89 일 때를 지수화를 하기되면 그 결과로 inf를 얻게 될 것이다.(for bfloat16 and float32) 이 결과 값이 attention operation의 최종 결과로 진행되기 때문에 numerical problem이 발생하게 된다.

score = 89인 경우

이러한 방법을 해결하기 위해 softmax는 모든 score에서 maximum score를 빼서 구현하는 방법을 사용한다. 이렇게 되면 softmax의 결과는 변경되지 않고 numerical problem은 피할 수 있다. 이 방법을 Parametric trick이라고 한다.

이를 구현해보면 다음과 같다.

https://eulertech.wordpress.com/2017/10/09/numerical-instability-in-deep-learning-with-softmax/

이 방법을 저자들이 제안하는 방법에 적용하기에는 아래와 같은 두 가지 문제점이 존재한다.

지수화된 score의 합계를 점진적으로 계산하면 최댓값이 sequence의 마지막 점수에 따라 달라질 수 있기 때문에 동일한 trick을 즉시 사용할 수 없다. 또한 score를 누적 합계에 더하기 전에 score를 지수화해야 하므로 빼기 역시 지연될 수 없다.
 
해당 두 가지 문제를 해결하기 위해서 저자들은 추가 scalar를 도입하여 incremental algorithm이 지금까지 확인한 amx score를 추적하고 필요에 따라 지수화된 값의 합을 renomalize 하는 방식을 적용하였다.
이를 적용한 방법으로 처리 순서를 정리하면 다음과 같다.

---

4. Code

이를 자세하게 확인해 보자.

1

2

3

4

이들은 JAX를 사용하였으며 병렬처리를 고려하여 O(√n) memory을 필요로 하는 code를 만들었다.
물론 O(log n)으로 전부 순차적으로 처리하도록 만들 수 있으나 이는 구현이 매우 복잡해진다고 한다.

---

5. Experiments

 

제안하는 방법을 사용할 시 더 긴 sequence data에서도 OOM이 발생하지 않는 모습을 보인다. 또한 기존의 방법보다 월등히 적은 memory를 사용함을 확인할 수 있다.

해당 성능지표를 통해 이들이 제안하는 방법을 사용을 하여도 기존 standard attention을 사용하였을 때와 성능의 차이가 없음을 확인할 수 있다.

---

본 논문은 계산 trick을 이용하여 기존의 attention에서 performance drop 없이 더 효율적인 space complexity를 사용할 수 있는 방법을 제시한다. ViT를 사용하는 연구를 진행하며 memory가 부족해 어려움을 겪고 있었는데 도움이 많이 되었다.
또한 기존의 attention module 자체를 바꾼 것이 아닌 softmax를 attention operation의 맨뒤로 보내어 연산 순서만 바꾸어 이러한 효과를 얻을 수 있다는 것이 매우 신기했다.
JAX를 통해 저자들이 구현을 해놓았기 때문에 JAX에 대한 관심도 생기게 하는 논문이었다.
본 논문에서 제안하는 algorthm은 활용도가 매우 높을 것 같기 때문에 더 자세히 공부하고 적용하여 modified를 해보도록 해야겠다.

---

Reference

https://madplay.github.io/post/time-complexity-space-complexity

시간복잡도와 공간복잡도(Time Complexity Space Complexity)

https://eulertech.wordpress.com/2017/10/09/numerical-instability-in-deep-learning-with-softmax/

Numerical instability in deep learning with softmax