3강 Binary Classification

< Logistic Regression? >

Logistic regression 은 label이 0, 1로 정해져 있는 이진 분류 문제에 사용되는 알고리즘이다.

 

Logitsic regression을 사용하여 데이터가 어떤 범주에 속할 확률을 0~1 사이의 값으로 예측하고 그 확률에 따라서 가능성이 더 높은 범주에 속하는 것으로 분류해 주는 supervised algorithm이다.

 

ex) 스팸 분류, 메일을 받았을 때 스팸일 확률이 0.5 이상이면 스팸, 0.5보다 낮은 경우 정상적인 이메일

수식으로 한번 확인해 보자.

Given X, want y' = P(y=1|X)

X (입력특성), y(주어진 입력특성 X에 해당하는 실제 값), y'(예측값)

즉, y'은 X가 주어질 때 y=1인 확률을 나타니며 0 <= y' <=1 사이의 값을 가진다.

 

X는 n_x 차원 상의 벡터를 의미하며 아래와 같이 표기할 수 있다.

Parameter W와 b는 각각 n_x 차원 상의 벡터와 실수이다.

이때 b는 interceptor를 의미한다.

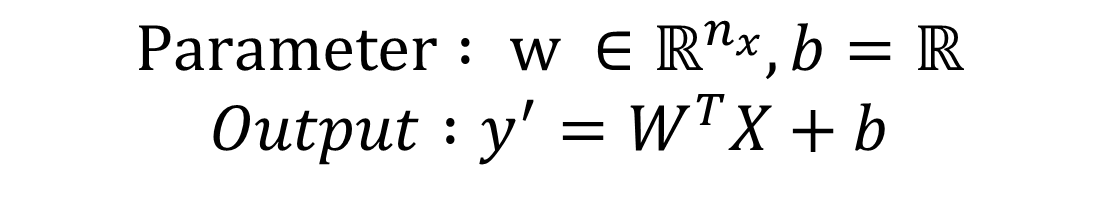
입력 x와 parameter w와 b가 주어졌을 때 위와 같이 y'을 구할 수 있다.

그러나 이러한 방법을 사용한 y'은 0~1사이를 벗어날 수도 있다는 문제가 생긴다.

지금 작업이 linear regression이였다면 그대로 사용하겠지만 binary classification을 위한 좋은 알고리즘은 아니다.

왜냐하면 y의 예측값이 y가 1일 확률이기 때문에 항상 0~1 사이여야 하기 때문이다.

위와 같은 output 수식은 음수가 나올 수도 있기 때문에 확률의 값이라고 하기에는 말이 되지 않는다.

 

그렇기 때문에 우리는 y의 출력값에 시그모이드 함수를 적용하여 출력된 값을 사용한다.

이때 σ 는 시그모이드 함수를 의미하며 수식은 아래와 같다.

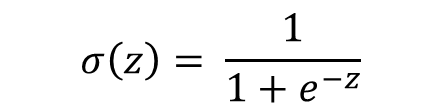
Sigmoid 수식

수평축이 z일 때 시그모이드 함수는 아래와 같은 형태를 가진다.

매끄럽게 그래프가 올라가며 수직축과 0.5에서 교차한다.

여기서 z는 아래의 수식을 의미한다.

< Logistic Regression Cost Function >

 

Logistic Regression의 수식과 입력그리고 우리가 원하는 최종 값을 간단히 정리해 보면 위와 같은 형태를 가진다.

즉, 실제값(y)에 가까운 예측값(y')을 구하는 것을 우리는 목표로 하고 있다.

 

이때 Loss(error) function은 어떻게 될까?

 

보통 loss function에서 많이 사용하는 수식은 아래와 같다.

제곱 오차

그러나 이는 logistic regression에는 적합하지 않다.

왜냐하면 이는 풀어야할 최적화 함수가 convex 하지 않기 때문에 여러 개의 local minmum을 가지게 되어 경사하강법을 통해 global minmum을 찾지 못할 수도 있기 때문이다.

그래서 제곱오차와 비슷한 역할을 하지만 최적화 문제가 convex해지는 다른 loss function을 사용한다.

Logistic regression의 loss function

이 함수를 직관적으로 이해하기 위해서 두 가지 경우로 나누어 생각해보자

 

1) y = 0인 경우

따라서 손실값을 최대한 줄이고 싶다면 마이너스 부호가 붙어 있기 때문에 log(1-y')이 최대한 커져야 한다.

그러기 위해서는 y'이 최대한 작아져야 한다. 이때 y'은 0~1 사이여야 하므로 y가 0이면 손실 함수는 y'이 0에 수렴하도록 매개 변수들을 조정할 것이다.

 

2) y = 1인 경우

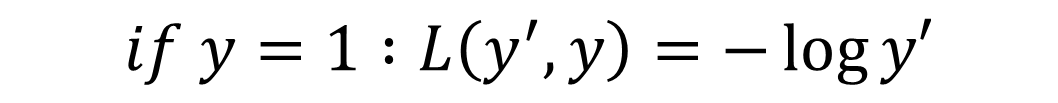
우리는 y=1 인경우 -log(y') 최대한 커지기를 원할 것이다. 그렇게 되기 위해서는 log(y')이 최대한 커져야 할 것이며 따라서 y'이 최대한 커져야 할 것이다.

하지만 이때 y'은 시그모이드 함숫값이기 때문에 예측값이 1보다 클 수는 없으므로 우리는 y'이 1에 수렴하도록 원한다라는 뜻이다.

 

 

하나의 입력에 대한 오차를 계산하는 함수를 손실 함수(loss function)라고 하며, 모든 입력에 대한 오차를 계산하는 함수는 비용 함수(cost function)라고 한다. 이때 cost는 매개변수의 비용처럼 작용한다는 의미를 가지고 있다.

따라서 비용 함수는 모든 입력에 대해 계산한 손실함수의 평균값으로 구할 수 있으며 이를 식으로 표현하면 아래와 같다.

결론적으로  Logistic Regression에서 의미하는 training 이란 비용함수 J를 최소화해 주는 매개변수 w와 b를 찾는 것이다. 그리고 이것이 우리의 목표이다.