Invariant Information Clustering for Unsupervised Image Classification and Segmentation

---

CVPR

---

Invariant Information Clustering for 

Unsupervised Image Classification and Segmentation

---

Xu Ji, Joao F. Henriques, Andrea Vedaldi

University of Oxford

---

지도학습의 학습된 task에 대해서 좋은 성능을 가진다는 것은 이미 많은 연구를 통해서 알려진 사실이다. 그러나 Labelled data를 구하기 힘든 분야의 경우 데이터가 충분하지 않아 학습이 어렵고 성능이 현저히 떨어진다는 문제점이 있다.

이런 문제를 개선하기 위해서 요즘 semi-supervised, self-supersied와 unsupervised의 연구가 활발히 이루어지고 있다.

또한 개인적으로 AI의 기술 개발의 마지막은 Artificial General Intelligence(AGI)이며 이의 실현을 위해서는 unsupervised가 필수적인 요소라고 생각하기 때문에 정말 중요한 deep learning의 학습 방법이라고 생각한다.

Unsupervised분야에서 Invariant Information Clustering(IIC)의 등장 이후 이를 대부분의 연구들이 이 방법을 활용하여 진행되고 있다고 한다. 꼭 알고 있어야 하는 논문이라고 생각한다.

 

Doi : 10.1109/ICCV.2019.00996

Invariant Information Clustering for Unsupervised Image Classification and Segmentation

---

1. Introduction

기존 대부분의 supervised deep learning은 많은 labelled data를 필요로 한다는 한계점을 가지고 있다. 그러나 labelled data는 구하기가 어려우며 특히 large-scale image classification 혹은 segmentation에서는 image를 labeling 하는데 많은 비용을 필요로 한다.

 

그렇기 때문에 unsupervised clustering에 대한 연구가 많이 진행되어 왔다. unsupervised clustering은 label없이 data point를 군집화 하는 것에 초점을 맞춘 방법이다.

과거에는 이를 위해 bootstrapping network training으로 k-means style을 결합하려는 시도가 많았으나 이는 오히려 성능의 저하를 가져오게 되었다. 이를 개선하기 위해 pre-training, feature post-preprocessing, clustering mecahnisms to the network 방법들이 연구가 되었다.

 

본 논문에서는 이러한 문제를 보다 원칙적으로 해결하기위한 방법인 Invariant Information Clustering (IIC)를 제안한다.

IIC는 임의로 초기화된 신경망을 label없이 end-to-end 학습을 하는 classification network이다.

IIC는 paird samples에 대한 function의 classicifation 사이의 multual information인 간단한 objective function을 포함하고 있다. input data는 모든 modality가 될 수 있으며 clustering space가 discrete 하기 때문에 mutual inforamtion을 정확하게 계산할 수 있다고 한다.

IIC의 전체 architecture

단순한 objective function을 사용하지만 기존 방법들의 두 가지 문제점에 강한 영향을 미치게 된다고 한다.

첫 번째는 single cluster가 prediction을 지배하거나 cluster가 사라지는 경향인 clustering degeneracy이다.

이는 k-means에서 관찰할 수 있으며 특히, representation learning과 결합할 때 잘 관찰되는 문제라고 한다.

이는 mutual inforation의 활용으로 개선할 수 있다고 한다.

Mutual information 내의 entropy 최대화 요소로 인해 모든 image를 동일한 class에 할당하면 손실이 최소화 되지 않으며 동시에 조건부 entropy 최소화로 인해 모델이 각 image에 대해 확실성(i.e. one-hot)이 있는 단일 class를 예측하는 것이 최적이다.

 

두 번째는 unknown and distractor classes가 있는 noisy data에 대한 문제이다.

이를 해결하기 위해서 IIC는 main output layer와 병렬로 auxiliary output layer를 사용한다. 이로 inference 시에 무시되는 overclustering을 생성하도록 유도한다고 한다.

 

정리해 보자면 IIC는 아래와 같은 두 가지 문제를 해결하였다.

1. Clustering degeneracy
2. noisy data with unknown or distractor classes

 

IIC의 학습 결과를 나타낸 그림

---

2. Method

우선 첫 번째로 이들이 성명하는 방법은 generic objecitve인 Invariant Information Clustering이다. 이는 unlabelled paired data를 위한 모든 종류의 clustering에 사용할 수 있는 방법이라 한다.

image clustering 및 segmentation에 적용하기 위해 paired data 생성을 필요로하고 이들은 random transformations와 spatial proximity를 활용하여 이를 생성하였다.

 

2.1 Invariant Information Clustering

x, x' ∈ X를 결합 확률 분포 P(x, x')의 paired data sample이라고 하자.

ex) x와 x'은 동일한 object를 포함하는 서로 다른 이미지일 수 있다.

Invariant Information Clustering(IIC)의 목표는 instance-specific details를 무시하면서 x와 x' 사이의 공통점을 보존하는 representation [Φ : X -> Y]를 학습하는 것이다.

이는 encoding된 변수들의 mutual information을 최대화 시키는 것으로 가능하다고 한다. 이를 식으로 표현하면 아래와 같다.

이는 Φ(x')에서 Φ(x)의 prodictability(예측 가능성)을 최대화하는 것과 같으며, 그 반대도 마찬가지라고 한다.

위 수식을 통해서 paired samples의 representation을 동일하게 만들수 있으며 이는 k-mean 처럼 단순히 representation distance를 최소화 하는 것과는 다르다고 이야기 하고 있다.

이때 위 식의 I는 entropy의 존재하는 degeneracy를 피하게 해준다.

 

Φ를 small output을 가지는 하나의 작은 neural network라고 생각해보면 위 식은 data에서 Instance-specific details를 폐기하는 효과가 있다.

Clustering을 진행하게되면 representation space가 Y = {1, ..., C}로 제한되어 있기 때문에 자연적인 병목현상(bottleneck)이 발생하게 된다. 이때 만약 용량이 무제한이라면 병목이 없는 상황을 가정할 수 있고 이는 Φ를 항등함수로 하여 쉽게 문제를 해결할 수 있다. i.e. I(x, x') ≥ I(Φ(x), Φ(x')).

 

하지만 이들의 목표는 deep neural network를 이용하여 representation을 학습하는 것이기 때문에, 이들은 soft clustering을 고려해야하며 이는 Φ가 softmax layer에 의해 종료됨을 의미한다.

Then, 아래의 수식을 통해 output Φ(x) ∈ [0, 1]^c는 C classes에 대한 이산 랜덤 변수 z의 분포로 해석할 수 있다.

이때 input에 할당된 cluster의 불확실성을 허용하기 위해서 output probabilistic을 만들어 준다.

 

이제 두 입력 x와 x'에 대한 cluster 할당 변수 z와 z'의 쌍을 생각해보자.

아래의 수식을 통해 이 변수들의 조건부 결합 분포를 구할 수 있다. 

이 수식은 특정 입력 x와 x'에 대해 조건화되었을 때 z와 z'이 독립적이라는 것을 나타내는 수식이다.

그러나 일반적으로 input pairs

i = 1, ..., n의 데이터 세트에 대한 marginalization 이후 독립적이지 않다.

예를 들어,

Φ = classification network

dataset = 이미지가 해당 쌍의 동일한 object를 포함하지만 무작위로 다른 위치에 있는 이미지 쌍각 쌍의 첫번째 class z로 구성된 무작위 변수는 두 번째 class z'로 구성된 무작위 변수와 강한 통계적 관계를 가지게 될 것이다. 즉, 하나는 다른 하나를 예측하므로 매우 의존적이라고 할 수 있다는 것이다.

 

이러한 문제를 해결하기위해서 dataset(or batch, in practice)에 대한 marginalization 후, 결합 확률 분포는 C x C 행렬 P에 의해 주어지며, 여기서  row c와 column c'의 각 요소는 아래 수식을 구성하게 된다.

The marginals

은 row와 colums의 합연산으로 얻을 수 있다.

일반적으로 대칭 문제를 고려할때, 각 (x_i, x'_i)에 대해 (x'_i, x_i)도 있으며 P는 (P+P^T)/2 를 사용하여 대칭된다.

위와 같은 방식을 적용하면 기존의 eq.(1)은 아래와 같이 계산할 수 있다.

 

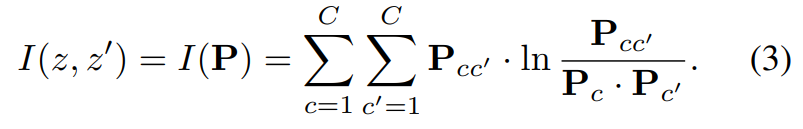
2.1.1. Why degenerate solution are avoided

Mutual Information (3)은 I(z, z') = H(z) - H(z|z')으로 확장될 수 있다.

따라서 이 양을 최대화하면 coniditional cluster assignment entropy H(z|z')을 최소화하고 개별 cluster assignment entropy H(z)를 최대화할 수 있다.

가장 작은 H(z|z')의 값은 0이며 이는 cluster 할당이 서로 정확하게 예측 가능할 때 얻을 수 있다.

가장 큰 H(z)는 ln(C)이며 이는 모든 군집이 동일하게 선택될 가능성이 있을 때 얻을 수 있다.

 

따라서 single cluster에 모든 samples가 할당된 경우(즉, 모든 샘플에 대해 output class가 동일하다.) loss가 최소화되지 않는다.

그러므로 mutual information의 최대화를 통해 예측 강화와 mass equalization이 자연스럽게 균형이 맞춰지므로, 이는 k-mean와 representation을 결합하는 알고리즘이 받기 쉬운 degenerate solution을 피하게 된다.

 

2.1.2. Meaning of mutual information

Mutual information의 최대화로 인해 얻을 수 있는 이점은 무엇이 있을까?

이는 크게 두 가지로 나누어서 확인할 수 있다.

 

첫 번째로 soft clustering으로 entropy만 최대화가 가능하다는 것이다. 이것은 모든 prediction vectors Φ(x)를 균일한 분포로 설정하여 얻을 수 있다.

 

두 번째로는 중복성을 공유하는 두 데이터 사이의 공통점을 찾는 것이다. 이는 공통점외에 나머지는 무시하면서 공통 부분의 distillation을 명시적으로 권장하는 효과낼 수 있다.

 

이는 모두 pairing sample을 사용하기에 가능한 점이라는 것을 기억해야 한다.

 

2.2. Image clustering

IIC는 paired samples (x, x')을 필요로 한다. 하지만 이는 unsupervised image clustering에서 종종 사용할 수 없는 경우가 생긴다.

이런 경우를 해결하기 위해 이들은 andomly perturbed version x'=gx로 구성된 generated image pairs를 사용하는 것을 제안한다. gx를 사용하면 아래와 같이 식을 다시 정의할 수 있다.

이때 image x와 transormation g는 모두 radom variabels이다.

이때 g에는 scaling, skewing, rotation or flipping (geometric), changing contrast and colour saturation (photometric), or any other perturbation that is likey to leave the content of the image intact가 포함될 수 있다.

 

IIC를 사용하여 쌍 중 어느것이 선택되었는지에 대해 변하지 않는 요소를 선택하는 것이 가능한데 이는 cluster를 삭제하지 않고 cluster가 perturbations에 닫히도록 분할하는 기능을 학습하는 것을 의미한다.

 

2.2.1. Auxiliary overclustering

특정 training datasets는 두 가지 유형으로 제공이 된다. 하나는 관련 class만 포함한 것이며, 다른 하나는 관련이 없거나 distractor class를 포함하는 것이다. 관련 class에 특화된 clustering을 학습하는 것이 바람직한데, 이는 distractor class가 제공하는 context에서 여전히 이익을 얻는다.

 

이들은 noisy image에 대한 solution으로 이들은 auxiliary overclustering head를 전체 데이터로 훈련된 network에 추가하고 main output head는 관련 class만 포함하는 subset으로 학습을 진행하였다.

이를 통해 unsupervised clustering 방법임에도 불구하고 nosie가 많은 unlabelled subset을 사용할 수 있게 되었다.

 

Auxiliary overclustering head는 ground truth 보다 더 많은 수의 cluster에 대한 예측을 출력하기 때문에 cluster의 main head와 일치하는 예측자를 계속 유지하면서 general feature representation을 학습하는데 유용하다.

 

2.3 Image segmentation

IIC를 image segmentation에 적용하기 위해서는 기존의 IIC에서 두 가지 modification이 필요하다.

우선 segmetation의 경우 각 pixel에 대한 예측이 조밀하게 일어나기 때문에 이미지 전체가 아닌 patch 단위의 clustering이 적용될 필요가 있다. 두 번째로는 전체 이미지와 달리 patch간의 spatial invariance(공간 관계)에 액세스할 수 있어야 한다.

따라서 이전 섹션 2.2에 geometric과 photonmetric invariances를 추가할 수 있다.

즉, synthetic perturbations(합성 섭동) 뿐만 아니라 이미지에서 인접한 patch 쌍을 추출하여 patch 쌍을 형상할 수 있다는 것을 의미한다.

 

patch단위로 gx를 생성할 경우 patch 개별 transform을 수행하는 것 보다 전체 이미지를 transform한 뒤 patch를 병렬로 변환하는 것이 훨씬 더 효율적이라고 한다.

 

위에서 말한 과정을 거치게되면 segmentation objective는 아래의 수식과 같이 표현할 수 있다.

이 수식 역시 mutual information을 최대화 하는 것을 목표로 하면 데이터 개수 n, transform g, pixel 개수 u에 대해 평균되어 사용한다.

---

3. Experiment

위 tabel 1은 기존의 방법들과 성능을 비교한 것이며 tabel 2는 ablation study를 진행한 결과이다.

이들이 제안하는 IIC가 더 가장 높은 성능을 가짐을 확인할 수 있다.

위 fig 5. 는 classification을 위한 clustering을 진행하였을 때의 결과를 시각화한 것이다.

위 tabe과 fig를 통해 semi-supervised를 진행한 것보다 이들이 제안하는 IIC의 성능이 더 좋음을 확인할 수 있다.

 

지금까지 classification의 성능을 확인해 보았다.

이를 통해 IIC가 기존의 unsupervised 혹은 semi supervised 보다 더 좋은 성능을 가짐을 확인할 수 있었다.

위 fig 7. 은 segmentation을 진행한 결과를 비교한 것이다.

위 tabel 4. 는 unsupervised segmentation을 진행한 성능을 나타내는 표이다.

IIC를 사용하였을때 비교적 기존의 unupervised 보다 더 높은 pixel accuracy를 가짐을 확인할 수 있다.

---

위 IIC는 현재까지도 많은 unsupervised 연구에 널리 사용되고 있는 방법이다.

mutual information을 최대화하는 방식이 학습에서 중요한 영향을 끼친다는 것을 확인할 수 있었다.

이는 앞으로 최신 unsupervised classification or segmentation paper를 이해하기 위해 반드시 알고 있어야하는 내용이라 생각한다.

---

Reference

https://hongl.tistory.com/170

Clustering - Invariant Information Clustering for Unsupervised Image Classification and Segmentation (1)