-
Bayesian Optimization Meets Self-DistillationAI/Vision 2024. 8. 9. 21:22
ICCV
Bayesian Optimization Meets Self-Distillation
Lunit Inc.
Auto ML과 self-distillation을 함께 진행하는 방법이다. 개인적으로 self-distillation을 이용한 연구를 진행하며 안정적으로 학습이 진행되는 hyperparameter(loss weight, lr scheduler gamma value, etc...)를 찾기가 어려워 grid search 이외에 다른 방법이 있나 찾아보다가 알게 된 논문이다. 실제로 연구에 적용을 해보지는 못했지만 흥미로운 논문이었다.
DOI: 10.1109/ICCV51070.2023.00163
CSDL | IEEE Computer Society
www.computer.org
0. Hyperparameter Optimization
Hyperparameter Optimization은 학습을 수행하기 위해 사전에 설정해야 하는 값인 hyperparameter(learning rate, batch size, etc...)의 최적값을 탐지하는 문제이다.
0.1 Manual Search
직관 또는 대중적으로 알려진 방법 등에 의존하여, 다음으로 시도할 후보 hyperparameter 값들을 선정하고, 실험하여 선택

학습률에 대한 Manual Search 과정에서의 불운한 결과 예시 출처: https://www.cognex.com/ko-kr/blogs/deep-learning/research/overview-bayesian-optimization-effective-hyperparameter-search-technique-deep-learning-1 위와 같은 Manual Search가 가는 문제점은 아래와 같다.
- 문제점 1) 다소 운에 좌우된다.
- 문제점 2) 한 번에 여러 종류의 hyperparameter를 탐색하고자 할 때 문제가 복잡해진다.
이를 개선하기 위해서 사용되는 보다 체계적인 방식으로는 Grid Search와 Random Search가 있다.
0.2 Grid Search
Grid Search는 탐색의 대상이 되는 특정 구간 내의 후보 hyperparameter 값들을 일정한 간격을 두고 선정하여, 이들 각각에 대하여 측정한 성능 경과를 기록한 뒤, 가장 높은 성능을 발휘했던 hyperparameter값을 선정하는 방법이다. 전체 탐색 대상 구간을 어떻게 설정할지, 간격의 길이는 어떻게 설정할지 등을 결정하는 데 있어 여전히 사람의 손이 필요하나, 앞선 Manual Search와 비교하면 좀 더 균등하고 전역적인 탐색이 가능하다는 장점 있다. 반면 탐색 대상 hyperparameter의 개수를 한 번에 여러 종류로 가져갈수록, 전체 탐색 시간이 기하급수적으로 증가한다는 단점이 있다.

학습률에 대한 Grid Search 과정에서의 불운한 결과 예시 출처: https://www.cognex.com/ko-kr/blogs/deep-learning/research/overview-bayesian-optimization-effective-hyperparameter-search-technique-deep-learning-1 0.3 Random Search
Grid Search와 큰 맥락은 유사하나, 탐색 대상 구간 내의 후보 hyperparameter 값들을 random sampling을 통해 선정
Random Search는 Grid Search에 비해 불필요한 반복 수행 횟수를 대폭 줄이면서, 동시에 정해진 간격 사이에 위치한 값들에 대해서도 확률적으로 탐색이 가능하므로, 최적의 hyperparameter 값을 더 빨리 찾을 수 있다.

학습률에 대한 Random Search 과정에서의 불운한 결과 예시 출처: https://www.cognex.com/ko-kr/blogs/deep-learning/research/overview-bayesian-optimization-effective-hyperparameter-search-technique-deep-learning-1
1. Introduction
우리가 기존 사용하든 CNN은 computer vision applications에서 좋은 성능을 달성하는 데 성공하였다. 그러나, CNNs의 성능은 hyperparameters의 선택에 의존적이라는 문제가 존재한다.
최적의 hyperparameters는 선험적으로 알려져 있지 않아, manual search를 필요로 한다. 보통 우리는 이를 찾기 위해서 많은 양의 실험을 해야 한다. 하지만, 이렇게 많은 시간을 사용하여 hyperparameters를 찾아도 모든 값에 대한 실험을 진행할 수는 없기 때문에일반적으로는 최적의 성능을 가진다고 보기는 어렵다. 또한 manual search를 보완하기 위해 나온 Grid and Random Search는 모두, 바로 다음번 시도할 후보 hyperparameter값을 선정하는 과정에서, 이전까지 조사 과정에서 얻어진 hyperparameter 값들의 성능 결과에 대한 "사전 지식"이 전혀 반영되지 않기 때문에 불필요한 탐색을 반복할 수 있다.
위와 같은 문제로 인해 매회 새로운 hyperparameter 값에 대한 조사를 수행할 시 "사전 지식"을 충분히 반영하면서, 동시에 전체적인 탐색과정을 체계적으로 수행할 수 있는 방법론으로, Bayesian Optimization (BO)가 제안되었다.
위와 같은 방식들의 문제를 해결하고자 제시된 Bayesian Optimization (BO)는 manual tuning을 자동화하고 성능의 경계를 허문 성공적인 접근 방법으로 각광받고 있다. OB는 관측에 기반한 유망한 구성을 제안함으로써 multi-dimensional search sapce의 효과적인 탐색을 가능하게 한다. BO는 본질적으로 hyperparameter 구성 및 해당 성능의 관측치를 사용하여 확률론적 이진 모델을 적합시키는 반복적인 프로세스이다. 각 반복에서 BO는 성능 향상의 가능성이 가장 높은 것으로 평가할 다음 구성을 제안한다. 제안된 구성으로 네트워크를 훈련한 후 새로운 관측치를 검색하여 확률 모델을 업데이트하는 데 사용된다. 이때, 이전 시도에서 얻은 부분적인 지식(즉, 훈련된 모델 및 해당 parameter 구성의 측정된 성능)만 전달되고 네트워크에서 학습된 지식은 폐기된다는 문제점이 있다.
Self-Distillation (SD)는 knowledge distillation 기법 중에 하나로, teacher model과 student model이 동일한 구조를 가지며, 동일한 모델 내에서 일어나는 knowledge distillation을 의미한다. 본연구에서는 SD를 knowledge transfer method로 볼 수 있다고 한다. 최근 연구에 따르면 이전에 훈련된 모델에서 동일한 용량으로 지식을 이전하면 모델의 성능을 향상할 수 있음을 보여주었다. 만약, student가 tearcher의 feature distribution을 모방하도록 훈련된다면, student가 teach을 능가할 수 있다. 논문 "Towards understanding ensemble, knowledge distillation and self-distillation in deep learning"에 따르면 이러한 현상을 이론적 및 실험적으로 다양한 모델을 앙상블 한 것과 유사한 효과로 해석하였다.
본 논문에서는 이러한 SD의 특성과 BO의 반복적인 특성에서 영감을 받아, 이전 시도에서 network 내부에 있는 지식을 BO과정의 다음 시도에 사용할 수 있는가? 에 대한 질문을 하게 되었다고 한다.
본 논문에서는 BO와 SD를 조합하여 이전 시험에서 얻은 지식을 완전히 사용할 수 있는 새로운 framework인 Bayesian Optimization meets Self-diStillation (BOSS)를 제안한다.

BOSS BOSS의 전체 프로세스는 위의 그림과 같다. BO 과정에 따라, BOSS는 성능을 향상할 가능성이 가장 높은 관찰을 기반으로 hyperparameter 구성을 제안한다. 그 후, 이전 시도에서 사전 훈련된 network를 선택하여 다음 SD 훈련에 사용하며, 이는 기존의 BO과정에서는 폐기되었던 부분이다. 이 과정은 반복적으로 수행되며, network가 이전 시도에서 지속적으로 개선될 수 있도록 한다.
이는 단순히 두 개의 독립적인 방법을 결합한 것이 아니라, 과거 지식(model parameter, hayperparameter 및 성능, etc..)을 적절하게 전이하는 문제에 대한 해결책을 제공한다. 제안된 해결책은 아래와 같다.
- Teacher 뿐만 아니라 Student도 사전 지식으로부터 초기화되어야 한다.
- 이전 시도에서 얻은 서로 다른 데이터를 바탕으로 초기화되어 사전 지식을 최대한 활용해야 한다.
2. Methold
2.1 Bayesian Optimization (BO)
2.1.1 Bayesian Optimization 기본
Bayesian Optimziation (BO)는 본래, 어느 입력값 x를 받는 미지의 목적함수 f를 상정하여, 그 함숫값 f(x)를 최대로 만드는 해 x'을 찾는 것을 목적으로 한다. 보통은 목적함수 표현식을 명시적으로 알지 못하면서 하나의 함숫값 f(x)를 계산하는데 오랜 시간이 소요되는 경우를 가정하며, 이러한 상황에서 가능한 적은 수의 입력값 후보들에 대해서만 그 함숫값을 순차적으로 조사하여, f(x)를 최대로 만드는 최적해 x'을 빨고 효과적으로 찾는 것이 주요 목표라고 할 수 있다.
BO의 필수 요소로는 Surrogate Model과 Acquisition function이 있다.
- Surrogate Model
현재까지 조사된 입력값과 함숫값 점들 (x_1, f(x_1)),..., (x_t, f(x_t)) 를 바탕으로, 미지의 목적함수 형태에 대한 확률적인 추정을 수행하는 모델이다. 가장 많이 사용되는 확률 모델은 "Gaussian Process (GP)"이며, GP 외에 많이 사용되는 모델은 "Tree-structured Parzen Estimators (TPE)"와 "Deep Neural Network (DNN)"등이 있다.
- Gaussian Process (GP)
GP는 어느 특정 변수에 대한 확률 분포를 표현하는 보통의 확률 모델과는 다르게, 모종의 함수들에 대한 확률 분포를 나타내기 위한 확률 모델이며, 그 구성 요소들 간의 결합 분포가 가우시안 분포를 따른다는 특징이 있다. GP는 평균함수 μ 와 공분산 함수 k를 사용하여 함수들에 대한 확률 분포를 표현한다.
- Tree-structured Parzen Estimators (TPE)
TPE는 일반적으로 잘 수행되고 범주형 및 연속 유형의 hyperparameter 모두에 활용할 수 있는 BO의 또 다른 변형이다.
3차 시간 복잡도를 갖는 GP와 달리 TPE는 선형 시간으로 실행된다. Hyperparameter 공간이 크고 교차 검증 점수를 평가하기 위한 예산이 매우 부족한 경우 TPE가 제안된다.
TPE는 아래와 같이 탐색 공간을 두 개의 분포로 나누어 접근한다.
l(x): 좋은 성능 (낮은 손실)을 나타내는 hyperparameter 값의 분포 g(x): 나쁜 성능 (높은 손실)을 나타내는 hyperparameter 값의 분포 이 두 분포는 각각의 hyperparameter에 대해 분리된 Gaussian Mixture Model로 표현되며, 주어진 loss 함숫값에 따라 hyperparameter들이 속할 분포를 결정한다. 이 방법은 GP 기반의 BO와 비교하여 고차원 공간에서도 효율적으로 탐색할 수 있다는 장점이 존재한다.
- Acquisition function
Surrogate Model이 목적 함수에 대하여 확률적으로 추정한 현재까지 결과를 바탕으로 바로 다음번의 함숫값을 조사할 입력값 후보 x_(t+1)을 추천해 주는 함수, 이때 선정되는 x_(t+1)은 최적의 x'를 찾는데 가장 유용할 만한 것이다.
2.1.2 Bayesian Optimization in BOSS
BOSS에서의 Bayesian Optimization (BO)는 위의 설명과 같이 일련의 hyperparameter λ 에 대해서 목적함수 Φ 를 최적화하는 것을 목표로 하는 iterative process이다. 각 iteration t에서, BO는 이전의 iterations의 관찰을 기반으로 Φ 에 근사화하는 Surogate model을 구축한다. 이때, 이전 반복의 관찰치 세트 Λ_(t−1) = {(λ_0,Φ(λ_0)),…,(λ_(t−1),Φ(λ_(t−1)))} 으로 표현된다. BO는 탐색함수(Acquisition function)은 μ(λ∣Λt−1) 을 사용하여 다음 hyperparameter 구성 λ_(t+1) 을 선택한다. 이 Acquisition function는 탐색과 활용의 균형을 유지하며, 가장 일반적으로 사용되는 것은 Expected Improvement (EI)이다. 이는 수식으로 표현하면 아래와 같다.

Acquisition function Expected Improvement (EI) 여기서 Φ_max 는 관찰된 최고의 함수 값이다. 반복 단계 t에서의 hyperparameter 구성은 아래의 수식과 같이 표현된다.

반복 단계 t에서의 hyperparameter 구성르 Φ(λ_t)를 평가한 후, 새로운 관찰치가 이전의 관찰치에 추가되어 아래와 같은 수식을 가지며, Surogate model은 업데이트 된다.

GP와 같은 많은 Surogate model 들이 p(Φ(λ) | λ)를 직접 모델리하는 반면, TPE는 p(λ | Φ(λ)) 를 모델링하며, 아래와 같은 두 개의 함수로 정의된다.

Tree-structured Parzen Estimator (TPE) 모델링 수식 Section 2.2.1에서 설명한 것과 같이 여기서 l(λ)는 성능이 threshold Φ* 보다 높은 관찰치들로 구성된 "good"density 이고, g(λ)는 나머지 관찰치들로 구성된 "bad" density이다. 이전 논문에서 EI를 최대화하는 것이
2.2 Self-Distillation (SD)
Self-Distillation (SD)는 동일한 architecture를 가진 teacher network가 student network로 지식 전달을 위한 방법이다.
무작위로 초기화 paraeters θ 를 가진 신경망 f가 주어지면, SD는 먼저 θ 에 대한 task loss L_gt(f(X ; θ), Y) 를 최소화하여 Teacher Model parameter θ^T 를 얻는다. 그 후, SD는 task loss L_gt와 distillation loss L_dt 사이의 균형을 유지하는 θ에 대한 loss를 최소화하여 student model의 θ^S의 parameter를 얻는다. 이 과정을 수식으로 표현하면 아래와 같다.

SD Loss 기존의 SD에서는 L_dt에 KL divergence loss를 사용하지만, 최근 연구에서 teach와 student의 logits간의 MSE가 더 나은 성능을 보인다고 밝혀졌다고 한다. 그렇기 때문에 해당 논문에서 저자들은 아래의 수식과 같이 MSE distillation loss를 사용하였다.

2.3 BOSS Framework
Bayesian Optimization meets Self-diStillation(BOSS)는 이전 시도에서 배운 지식을 통합하기위해 SD를 BO process에 통합한다. 제안된 framework는 다양한 BO 및 SD 방법에 적용할 수 있지만, 계산 복잡성이 낮고 다양한 탐색 공간에 확장 가능한 TPE를 선택하였다고 한다. 또한 위에서 설명하였듯 KL-Divergence 보다 더 나은 성능을 보이며 hyperparameter가 적게 요구되는 것으로 밝혀진 MSE를 distillation loss로 사용하였다고한다. BOSS의 전체 알고리즘은 아래와 같다.

BOSS의 전체 알고리즘 순서 SD를 수행하기 위해서는 student network 를 훈련시키기 위한 teacher network 가 필요하다. 그러나, 초기에는 network가 없기 때문에 cold start proble이 발생한다. 이 문제를 해결하기 위해 warm-up 단계를 도입되며, 이는 일반적인 BO process와 유사하지만 훈련된 CNN을 후속 단계에서 사용할 수 있도록 기록해둔다. Warm-up 단계에서는 random parameter θ 로 초기화하고, hyperparameter λ 가 수식(1)에서와 같이 아래와 같은 acquisition 함수를 사용해 제안된다.

acquisition function 그런 다음 training image X와 해당 label Y를 사용하여 task loss L_gt를 최소화하여 λ에 대한 새로운 parameter θ* 를 얻는다. 이때, image classification에서 사용되는 cross-entropy loss 와 같은 task-specific loss가 사용될 수 있다. 훈련 후, neural network의 성능 Φ(λ) 가 계산되고 관찰치 (λ, Φ(λ)) 가 관찰치 세트 Λ에 추가된다. 또한, 얻어진 parameter θ* 는 parameter set Θ에 추가된다.
BOSS training이 수행되는 두 번째 단계에서는 training 방식이 준비 단계와 다르고 최적의 구성이 다를 가능성이 있다. 그러므로, 새로운 관찰치 세트 Λ'이 빈 상태로 초기화 된다. Parameter set Θ 와 사전에 정의된 후보자 수 K를 기준으로, 성능에 따라 상위 K개의 후보가 결정된다. 그 중 두 개를 무작위로 다시 선택하여 student와 teacher를 정의한다. Teacher θ_T와 sudent θ_S 를 서로 다른 parameter로 초기화하는데, 이는 서로 다른 network에서 얻은 지식을 결합하여 이익을 얻을 수 있을 것으로 기대하기 때문이라 한다.
초기화 후, hyperparameter λ 는 warm-up 단계와 동일한 절차로 제안된다. Warm-up 단계와 달리, θ는 식 (3)의 손실을 최소화하도록 training 된다.

SD Loss 훈련이 완료되면 성능과 trained parameter가 각각 Λ'와 Θ 에 추가된다. 이 절차는 budget N이 소진될 때까지 반복된다. Pre-trained weight의 활용이 BO의 모델링에 방해가 될 수 있다는 잠재적인 문제점에도 불구하고, 이전 연구에서는 BO가 각 시도에서 weights를 무작위로 초기화하여 초기 weights의 변동성에 충분히 강건하다는 것을 입증했다.
BOSS의 training이 진행됨에 따라, top-K model은 이전 시도의 knowledge를 통합한 model로 업데이트된다. 이 model들은 후속 반복에서 지식을 전이하는 데 사용되며, 향상된 network 후보를 반복적으로 업데이트하므로써, BOSS는 이전 시도에서 지속적으로 성능을 향상시킬 수 있고 한다.
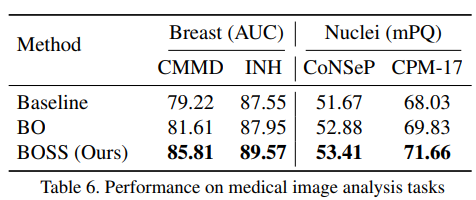
3. Experiments





'AI > Vision' 카테고리의 다른 글